Optics Tutorial
An understanding of optics and optical instruments is required for the following experiments: Atomic Physics, Atom Trapping, CO2 Laser, Quantum Interference & Entanglement, and Nonlinear Spectroscopy and Magneto-Optics. In each case, the text by Melissinos is an excellent exposition for specific instruments. The best general reference is Jenkins and White, Fundamentals of Optics, although any current optics book is of help, including some at the sophomore physics level.
Contents |
Supplemental Optics Training Fundamentals from CVI Melles Griot
Fundamental Optics (58 pages)
Introduction to Laser Technology
Handling Optics
Proper handling of optical elements is very important to avoid damage. The following rules follow directly from common sense:
- If disassembling optics, place it such that it is protected and cannot be scratched. Consider leaving it in its mount as it is usually well protected. If you do so bolt the mount to the table such that it cannot fall over. Alternatively, you might place the optics wrapped in a lense tissue or on a lense tissue inside a clean box. Note that scratching and chipping off material could destroy the device entirely.
- Do not touch the functional surfaces of the optical elements. Dirt and oil from the skin contaminates the surfaces severely. When you cannot avoid touching, always hold them from the side. Avoid using tweezers or any tools which can scratch the optics. If you need to use Allen keys or similar tools near the optics, take extreme care not to slip off and scratch the surface.
- Do not clean the mirrors, lenses and waveplates unless advised to do so. Cleaning the high quality surfaces without causing permanent damage requires special equipment and procedures.
- Cover optics up if not in use. This will reduce dust and the chance to damage the optics during cleaning.
- Avoid stress on the optical fibers. Bending it too much will destroy a fiber easily even though you might not notice any damage from the outside (the holds true for BNC cables, too).
Lenses
We need a lens when we want to form an image of an object. Note: The correct singular spelling is lens, although the plural is lenses. Here's what you should know about lenses:
Positive lenses can form real images, as in a camera.
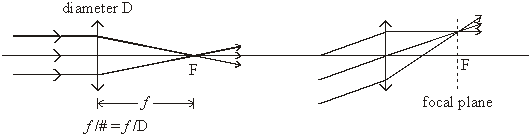
A lens has a focal length, which can be found by forming an image of a distant object, such as the sun, and measuring the distance from the lens to the image. The focal plane is a plane perpendicular to the axis and placed at the focal length away from the lens. Off axis objects are focused on the focal plane.
The ratio of the focal length to the diameter of the lens is a measure of how "fast" the lens is, which can be thought of as how much light the lens collects. For example, a lens 50 mm in diameter with a focal length of 250 mm is called an "f five lens", or to have an f-number of five, written f/5.
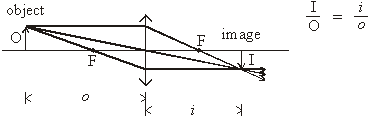
The relationship between focal length, object distance (o), and image distance (i) is given by 1/o + 1/i = 1/f. To form a real image, o must be greater than f. A real image is inverted, upside down, when compared to the object. The ratio of object size to image size is i/o. The smallest distance between object and image is 4f - four times the focal length.
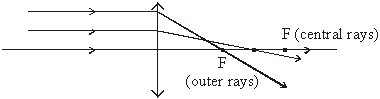
The quality of the image - how accurately it represents the object - depends on the type of lens and on its f/number. A simple single element lens suffers from spherical aberration. Light passing through the outer zone (near the outer edge) of the lens has a shorter focal length than light passing through the central zone or portion of the lens. As a consequence, the image is fuzzy when a large f/number single element lens is used to form an image.
A single element lens also suffers from chromatic aberration. Different colors of light have different focal lengths - blue the shortest, red the longest. Every image has a colored halo around it, although often it is not noticeable.
An achromatic doublet lens has two elements cemented together, one a positive lens and the other a negative lens. The chromatic aberration is almost completely corrected for, and at the same time spherical aberration is reduced nearly to zero. Whenever possible, use achromatic doublets.
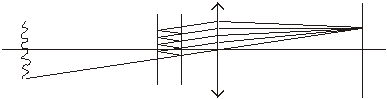
The drawings illustrate how a lens might be used. Calculate in advance where a lens should be placed, but remember that the final placement is always determined experimentally.
Mirrors
Optically speaking, mirrors and lenses are interchangeable. Take any given positive lens, split it in half, coat the flat surface with a reflecting material, and you have the equivalent of a concave mirror. The focusing properties are the same, the equation 1/o + 1/i = 1/f is the same. The light path is the same except that it is folded. BUT, a mirror has spherical aberration, which is not easily correctible, and it has no chromatic aberration (an important advantage)
Spectrometers
A spectrometer is used to discover what frequencies or wavelengths are present in radiation. It contains a dispersive element, which separates out radiation according to frequency, often by changing the direction of propagation of some other parameter of the light to make the separation observable.
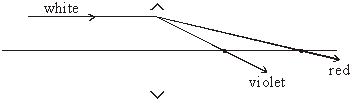
For example, white light incident on a prism is dispersed at different angles according to the wavelengths present in the radiation, as illustrated. A single ray is deviated according to wavenumber, with red deviated the least and violet the most in the visible spectrum.
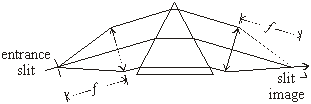
When a wavefront rather than a ray is incident on the prism, the dispersed wavefronts overlap, so an optical system is necessary to separate the dispersed wavenumbers. A useful optical system has an entrance slit, and forms an image of this slit at the output, where we can put a photographic film or a scanning detector.
For a very small entrance slit, the width of the exit slit (the image of the entrance slit) is dependent on the width of the wavefront rather than on the width of the slit, because of diffraction. It's like a single slit diffraction pattern, where the angular half-width of the pattern is given by $ \sin{\theta}=\frac{d}{\lambda} $. The physical width of the diffraction pattern of the slit is given by $ f \cdot \theta $.
In practice, the entrance slit is set to the same width as the diffraction pattern width for a vanishingly small entrance slit. Any larger slit increases the width of the diffraction pattern and any smaller one reduces the amount of light admitted to the spectrometer.
Most spectrometers use a diffraction grating instead of a prism, but the optics are the same.
Diffraction Gratings
In several of our 111 laboratory experiments we need to disperse a beam of light into its various colors. We could pass it through a prism and see the colors, but more commonly we use a diffraction grating to produce a spectrum as described above. It is inserted into an optical system in place of the prism in the previous example.
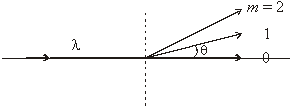
The grating disperses the light according to wavelength, with red light dispersed the most and violet the least. The grating equation is $ m\cdot\lambda=d\cdot\sin{\theta} $. We customarily use gratings in the first order.
When a diffraction grating is placed in the system shown, the central image of the slit (m = 0 at $ \theta $ = 0) remains unchanged from the "no grating" condition, but now other slit images are formed at angles corresponding to different wavelengths of light according to the grating equation.
We assume you learned about diffraction gratings in Physics 7. To refresh your memory and increase your knowledge and understanding, refer to Jenkins and White, Fundamentals of Optics. However, most gratings are reflection rather than transmission gratings. The optical system is shown below. Remember that mirrors are like lenses except that they fold the light path.
When analyzing a spectrum, we want to know what wavelengths are present and their relative intensities. The smallest wavelength separation we can observe is characterized by the resolving power R, which is written as $ R=\frac{\lambda}{\triangle\lambda}=mN=\frac{W\sin\theta}{\lambda} $. N is the number of grooves in the grating (width of grating $ W=N\times \mbox{groove spacing} $). A 3 cm wide grating with 600 grooves/mm when used at an angle of 10 degrees in the first order to view the green line of mercury at 546.1 nm has a resolving power of R = 90 000.
The dispersion is given by $ \frac{d\theta}{d\lambda}=\frac{\tan\theta}{\lambda} $, or the inverse linear dispersion (called plate factor) by $ \frac{d\lambda}{dl}=\frac{\lambda}{f\tan{\theta}} $, usually expressed in units of nanometers/millimeter. The plate factor in the previous example when the spectrometer has a focal length of 50 cm is 6.6 nm/mm.
The Atomic Physics (Balmer Series) spectrometer is set up as shown above. The focal length is 50 cm.
The Laser Induced Fluorescence spectrometers are similar, but have a focal length of 25 cm.
The grating in the Carbon Dioxide Laser is placed in the beam path between the two laser mirrors. The beam size is small and doesn't nearly fill the grating. The resolution is very low, but adequate for the purpose at hand.
Interferometers
A diffraction grating splits a single wavefront into many parts or pieces, and contrives to have the parts interfere, thereby creating a spectrum of the radiation. The process is called wavefront division.
An interferometer takes the entire wavefront and splits off one or more copies of it with smaller amplitudes but the same spatial dimensions - each split-off wavefront is the same size as the original wavefront. This process is called amplitude division. These wavefronts are then guided to interfere with one another.
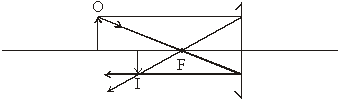
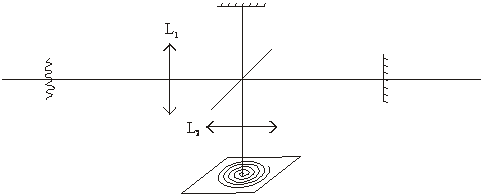
A Michelson interferometer splits the incoming wavefront into two wavefronts of equal amplitudes and then causes them to interfere.
With the optics as shown, the source can be of any size. The first lens can be omitted. At the image plane a series of rings is formed, each of a different order of interference given by $ m\lambda=2t\cos{\theta} $. At the center of the pattern $ m=\frac{2t}{\lambda} $, and m gets smaller as $ \theta $ gets larger (out from the center of the pattern). When one mirror is displaced or moved, the rings grow from the center when the path length is increased, and collapse into the center when the path is decreased. When the entrance aperture is circular and of a size to cover only one ring, the detector output is a cosine curve as the path difference is changed. This cosine-curve output, one for each frequency in the incoming light, is called the interferogram. To get the spectrum, the Fourier transform of the interferogram must be calculated. The resolving power is given by $ R=\frac{2t}{\lambda} $, and the resolution or resolving limit is given by 1/2t in cm-1. An interferometer with a mirror travel of 10 cm has a resolving limit of 0.05 cm-1, and a resolving power of 300 000 for a wavelength of about 700 nm.
Such a spectrometer is called a Fourier transform spectrometer, or FTS for short. The most useful high-resolution spectrometers are of this type.
With a laser as a source of light, there is no need for either of the lenses, since the laser beam is already collimated and the ring pattern at the output is clearly visible. This is true even when a lens is used to expand the beam.
A Fabry-Perot interferometer consists of two plane-parallel reflecting surfaces spaced a distance $ t $ apart. Here, the wavefront is divided as in the Michelson interferometer, but into many wavefronts whose amplitudes are steadily decreasing with each division (due to reflection at the surfaces). Instead of a two-beam interference problem, there is an N-beam interference.
For example, when each plate has a reflectance of R = 0.9 (90% of the light is reflected, 10% transmitted), the effective number of interfering beams is N = 30. The resolving power is $ \frac{2Nt}{\lambda} $, which is N times the resolving power of a Michelson interferometer. For example, with a spacing of 1 cm and a reflectance of 0.9, a Fabry-Perot interferometer has a resolution for the mercury green line of 1 100 000, or a resolving limit of 0.017 cm-1.
In the Atomic Physics experiment (Zeeman Effect) we examine the circular fringe pattern visually, although it can be photographed, and some instruments can scan by moving one plate. The concept of overlapping orders is important here. Two wavelengths can appear at the same angle but in different orders. When the orders differ by 1, the difference in wavelengths is called the free spectral range. It can be expressed in either wavelengths or wavenumbers. In wavenumbers, it is equal to 1/2t, or 0.5 cm-1 in the example given above. Melissinos has an especially good discussion of the Fabry-Perot interferometer.
Lasers
We use Helium-Neon and Argon Ion lasers as tools in our laboratory, and we have an experiment with a CO2 laser. Each of these gas lasers has an optical cavity. The cavity is like a Fabry-Perot interferometer - two highly reflecting mirrors spaced widely apart, in our case nearly a meter for the CO2 laser, about 50 cm for the argon ion laser, and 20 cm for the helium-neon laser. The line widths of the radiation for each of these lasers depend not only on the optical characteristics of the cavity (interferometer) but also on the nature and conditions of the active medium inside. You will have to read more specific references in order to understand how the widths come about.
Polarization Optics
Light, of course, refers to propagating spatial and temporal modulations of the electric and magnetic vector fields. The vector nature of these fields gives freedom for light to be described not only by its amplitude, propagation direction, and frequency, but also by its polarization.
In isotropic media (most media with which you are familiar), the electric and magnetic vector fields that comprise plane waves of light are oriented in the plane transverse to the direction of propagation. Each component of those vectors oscillates about a mean value of zero. To describe such a wave, it is helpful to keep track of just the electric field (the behavior of the magnetic field is then determined by Maxwell's equations), and, moreover, to represent that field as a complex vector, $\tilde{\mathbf{E}}$, with the implication that the real electric field is described as $\mbox{Re} \,\tilde{\mathbf{E}}$.